Phương pháp tính thể tích

Phần I.                       THỂ TÍCH KHỐI CHÓP – KHỐI LĂNG TRỤ

            Trong trường phổ thông, Hình học không gian là bài toán rất khó đối với học sinh, do đó học sinh phải đọc thật kỹ đề bài và từ đó xác định giả thiết bài toán, vẽ hình rồi tiến hành giải bài toán.

            Cả chương trình chuẩn và nâng cao đều đề cập đến thể tích khối đa diện (thể tích khối chóp và khối lăng trụ)

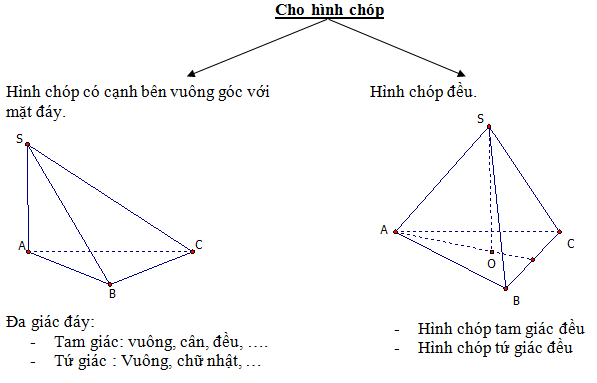
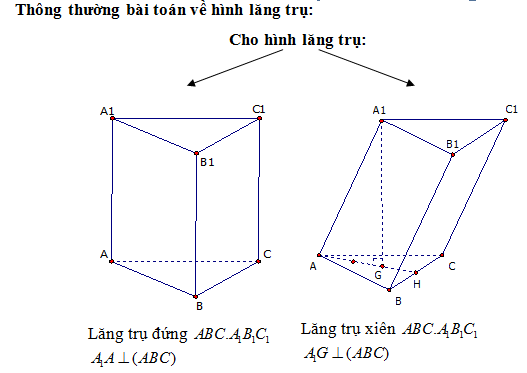
            Thông thường bài toán về hình chóp được phân thành hai dạng như sau:

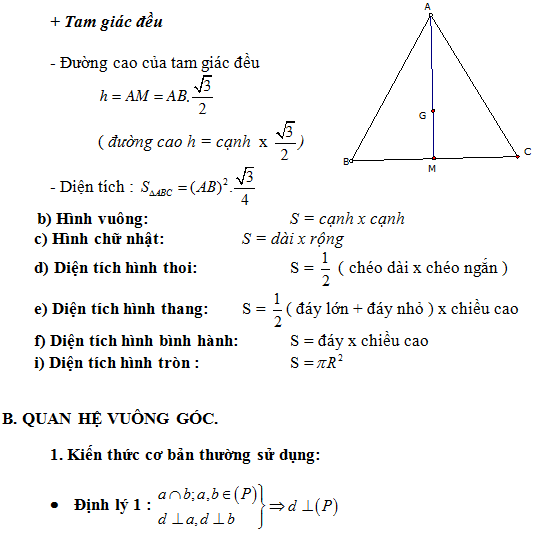
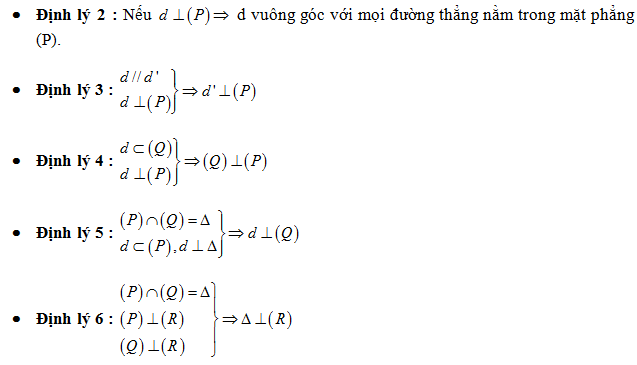
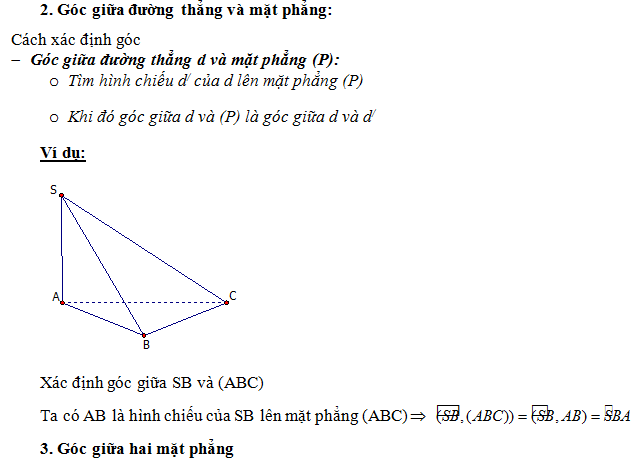
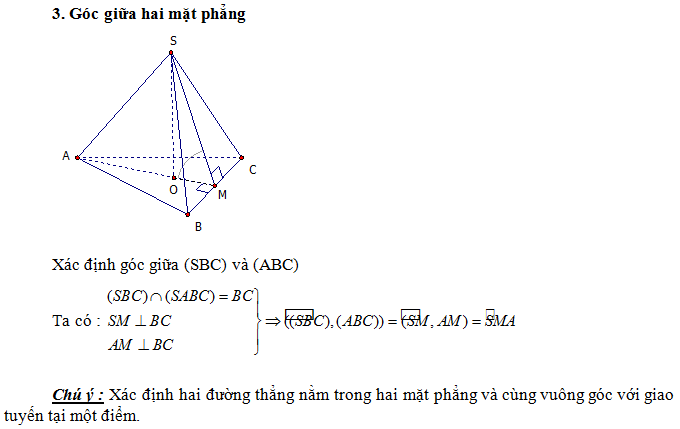
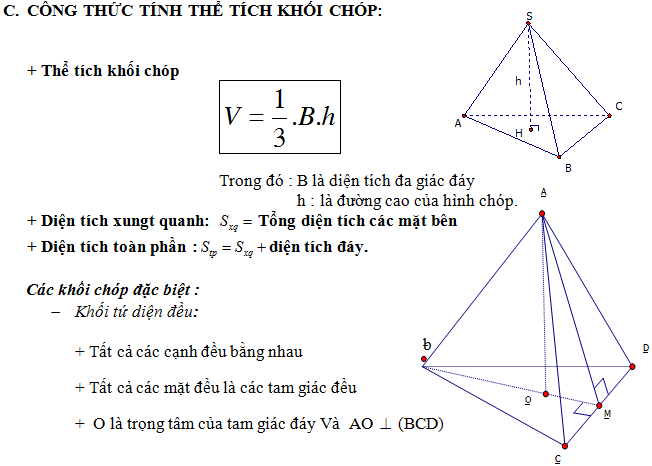
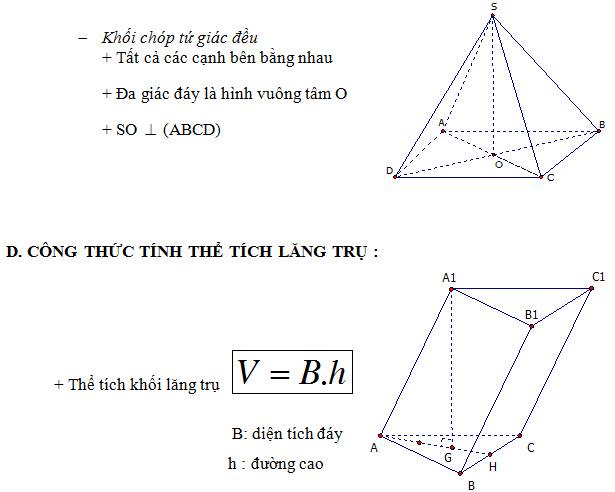
E. TỶ SỐ THỂ TÍCH

- Việc tính thể tích của một khối chóp thường học sinh giải bị nhiều sai sót, Tuy nhiên trong các đề thi lại yêu cầu học sinh tính thể tích của một khối chóp “nhỏ” của khối chóp đã cho. Khi đó học sinh có thể thực hiện các cách sau:

+ Cách 1:

• Xác định đa giác đáy
• Xác định đường cao ( phải chứng minh đường cao vuông gới với mặt phẳng đáy)
• Tính thể tích khối chóp theo công thức

+ Cách 2

• Xác định đa giác đáy
• Tình các tỷ số độ dài của đường cao (nếu cùng đa giác đáy) hoặc diện tích đáy (nếu cùng đường cao) của khối chóp “nhỏ” và khối chóp đã cho và kết luận thể tích khối cần tìm bằng k lần thể tích khối đã cho

+ Cách 3: dùng tỷ số thể tích

Hai khối chóp S.MNK và S.ABC có chung đỉnh S và góc ở đỉnh S

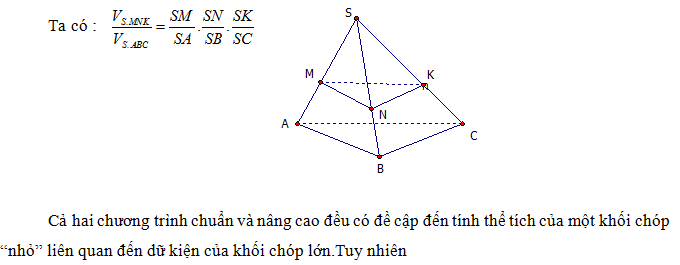
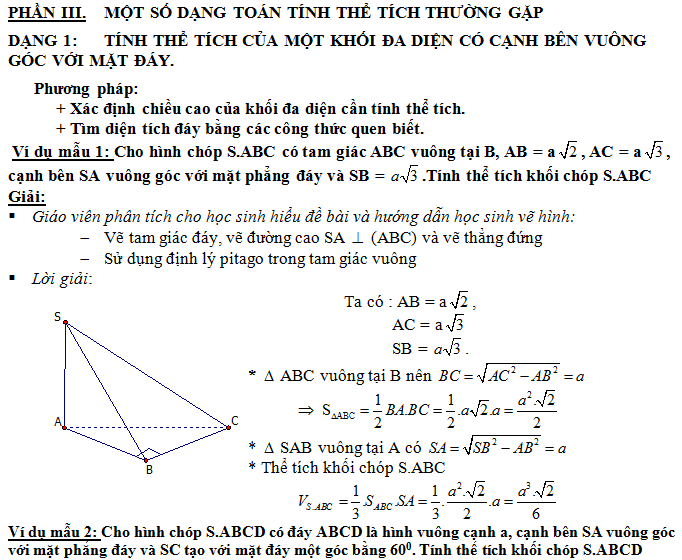
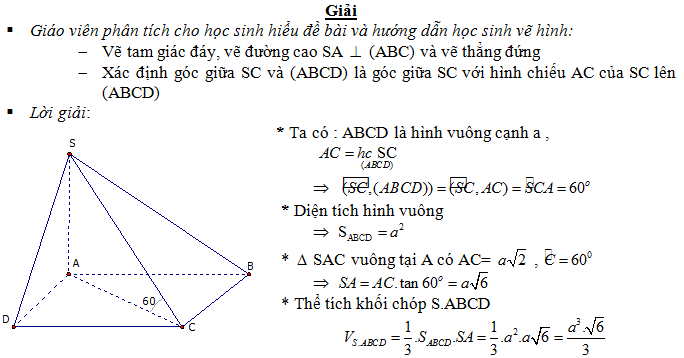
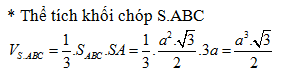
• Nhận xét:

-     Học sinh không lý luận để chỉ ra góc nào bằng 60^o, do đó mất  điểm.

-     Học sinh xác định góc giữa hai mặt phẳng bị sai vì đa số học sinh không nắm rõ cách xác định góc và cứ hiểu là góc SMA với M là trung điểm BC

• Nếu đáy là tam giác vuông tại B (hoặc C), hình vuông và SA vuông góc với đáy thì góc giữa mặt bên và mặt đáy sẽ là góc được xác định tại một trong hai vị trí đầu mút của cạnh giao tuyến
• Nếu đáy là một tam giác cân (đều) và SA vuông góc với đáy hoặc là hình chóp đều thì góc giữa mặt bên và mặt đáy là góc ở tại vị trí trung điểm của cạnh giao tuyến.