Tìm m để hàm số đạt cực trị
Cập nhật lúc: 14:00 19-06-2015 Mục tin: LỚP 12
Xem thêm:
CỰC TRỊ CỦA HÀM BẬC 3
Bài toán tổng quát: Cho hàm số y = ax3 + bx2 + cx + d (a ≠ 0, a, b, c, d phụ thuộc vào tham số). Tìm giá trị của tham số để hàm số có cực đại, cực tiểu (cực trị) thỏa mãn điều kiện cho trước.
Phương pháp:
Bước 1: Tính y’ = 3ax2 + 2bx + c, y’ = 0 ⇔ 3ax2 +2bx + c = 0 (1)
Để hàm số có cực đại, cực tiểu ⇔ y’ = 0 có hai nghiệm phân biệt ⇔ (1) có hai nghiệm phân biệt
\(\left\{\begin{matrix} a\neq 0 & \\ \Delta (\Delta ')\neq 0 & \end{matrix}\right.\)⇔ Giá trị tham số thuộc miền D nào đó (*)
Bước 2:
Từ điều kiện cho trước dẫn tới một phương trình hoặc một bất phương trình theo tham số, giải phương trình này ta được tham số sau đó đối chiếu với điều kiện (*) và kết luận.
Một số điều kiện thường gặp:
- Để hàm số y = f(x) có 2 cực trị <=> \(\left\{\begin{matrix} a\neq 0 & \\ \Delta _{y'}>0 & \end{matrix}\right.\)
- Để hàm số y = f(x) có 2 cực trị nằm về 2 phía đối với trục hoành <=> \(y_{CD}.y_{CT}<0\)
- Để hàm số y = f(x) có 2 cực trị nằm về 2 phía đối với trục tung <=> \(x_{CD}.x_{CT}<0\)
- Để hàm số y = f(x) có 2 cực trị nằm phía trên trục hoành <=> \(\left\{\begin{matrix} y_{CD}+y_{CT}>0 & \\ y_{CD}.y_{CT}>0 & \end{matrix}\right.\)
- Để hàm số y = f(x) có 2 cực trị nằm phía dưới trục hoành <=> \(\left\{\begin{matrix} y_{CD}+y_{CT} <0& \\ y_{CD}.y_{CT}<0 & \end{matrix}\right.\)
- Để hàm số y = f(x) có cực trị tiếp xúc với trục hoành <=> \(y_{CD}.y_{CT}=0\)
- Đồ thị có 2 điểm cực trị khác phía đối với đường thẳng d: Ax +By +C = 0

Chú ý: Khi thay đường thẳng d bằng trục Ox hoặc Oy hoặc một đường tròn thì vẫn áp dụng kết quả trên . Các kết quả khác thì tùy từng điều kiện để áp dụng.
VÍ DỤ MINH HỌA
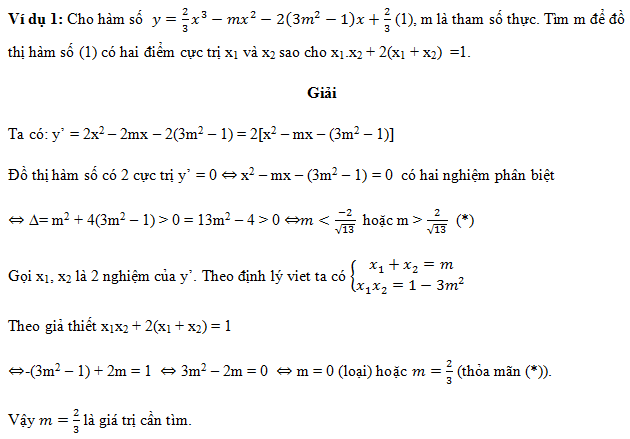

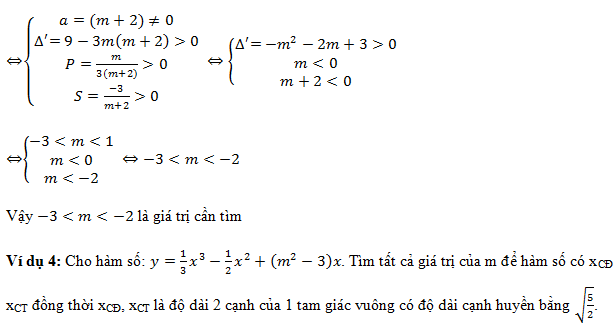
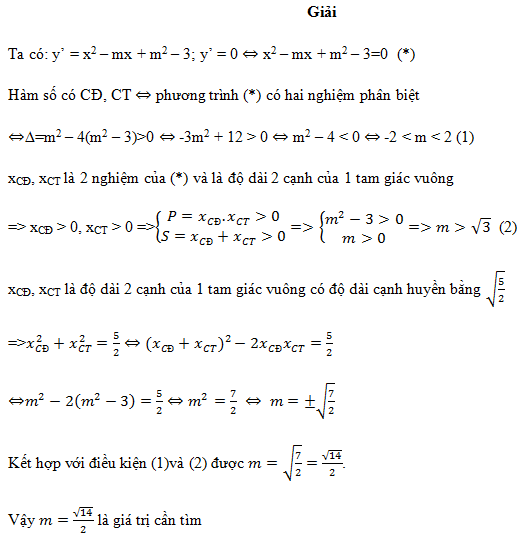
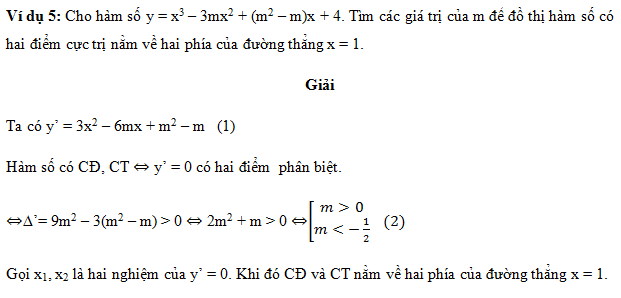
Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
-
Cách tìm cực trị của hàm số(03/06)
Cực trị của hàm số là một phần rất quan trọng thường xuyên gặp trong đề thi ĐH - THPT QG môn Toán nhất là những năm gần đây. Bài viết này sẽ giúp các em hình dung được các bước tìm cực đại, cực tiểu của hàm số một cách tổng quát và dễ nhớ nhất.
-
Cực trị hàm số bậc 3 (có lời giải chi tiết)(05/06)
Cực trị của hàm số bậc 3 là một phần thường xuyên gặp trong câu bài toán liên quan đến khảo sát hàm số. Phần này tương đối là đa dạng. Bài viết sau đây sẽ hỗ trợ cho các em cách giải chi tiết của từng dạng bài một trong phần này giúp các em nắm chắc 1 điểm phần câu 1b trong đề thi ĐH - THPT QG môn Toán nhé!
-
Để đạt được điểm 7 môn Toán(03/06)
Để đạt được điểm 7 trong 4 tháng luyện thi đại học không phải là dễ dàng. Tài liệu này đã được tinh giảm chỉ còn phần những kiến thức cần thiết cơ bản bao gồm toàn bộ 9 hệ thống kiến thức lớn ôn luyện thi ĐH - THPT Quốc Gia môn Toán giúp các em đạt được điểm cao trong kỳ thi chung này.
-
Ôn tập khảo sát hàm số ( đầy đủ )(27/05)
Phần này sẽ giúp các em ôn lại toàn bộ các dạng bài trong chương khảo sát sự biến thiên và vẽ đồ thị hàm số hay nhất và đầy đủ nhất.
-
20 câu hỏi trắc nghiệm về cực trị hàm số - có lời giải chi tiết.(09/08)
Bài viết gồm 20 câu trắc nghiệm có đáp án và lời giải chi tiết. 20 câu này gồm các dạng hàm phân thức bậc nhất trên bậc nhất, hàm số bậc 3 và hàm bậc 4 giúp các em làm quen được nhiều dạng toán. Hơn nữa, trong phần lời giải chi tiết có các phương pháp giải tự luận nắm chắc kiến thức và cả phương pháp giải nhanh trắc nghiệm nhằm giúp các em có thể hiểu bài sâu hơn và làm được những bài tập tương tự khác.
-
Tổng hợp những bài toán liên quan đến cực trị của hàm số - có lời giải(18/08)
Một số dạng toán thường gặp trong phần cực trị của hàm số như: Các quy tắc tìm cực trị của hàm số, tìm m để hàm số đạt cực trị thỏa mãn điều kiện cho trước, tìm điều kiện để hàm số đạt cực trị tại x0; tìm m để hàm số không đạt cực trị, viết phương trình đường thẳng đi qua 2 điểm cực trị.
-
Tìm cực trị của hàm số và tìm tham số m để hàm số đạt cực trị thỏa mãn điều kiện cho trước(15/08)
Tìm cực trị của hàm số và tìm tham số m để hàm số đạt cực trị thỏa mãn điều kiện cho trước. Bài toán cực trị thường gặp nhất trong các đề thi cao đẳng, đại học, THPT QG môn Toán. Đây là phần kiến thức có rất nhiều vấn đề cần học.
-
Một số dạng toán liên quan đến khảo sát hàm số (có lời giải)(22/06)
Bài viết giới thiệu về một số dạng thường gặp nhất trong phần khảo sát sự biến thiên và vẽ đồ thị hàm số như: xét chiều biến thiên, cực trị của hàm số, tìm giá trị lớn nhất, nhỏ nhất của hàm số...
-
Các dạng toán cực trị hàm số cơ bản và nâng cao(22/06)
Trong bài viết trước chúng ta đã biết cách tìm cực trị của một hàm số. Tiếp theo chúng ta sẽ tìm hiểu một số dạng bài tập liên quan đến cực trị hàm số cơ bản và nâng cao. Các bài tập này chủ yếu là tìm tham số m để hàm số có cực trị thảo mãn một yêu cầu nào đó. Ta thường gặp một số dạng như sau:
-
Tìm điều kiện để hàm số có cực trị(06/08)
Tìm m để hàm số đạt cực đại, cực tiểu theo yêu cầu bài toán rất dễ gặp trong các đề thi THPT Quốc Gia nên chúng ta cần phải nắm chắc.

