Trong bài viết trước chúng ta đã biết cách tìm cực trị của một hàm số. Tiếp theo chúng ta sẽ tìm hiểu một số dạng bài tập liên quan đến cực trị hàm số cơ bản và nâng cao. Các bài tập này chủ yếu là tìm tham số m để hàm số có cực trị thảo mãn một yêu cầu nào đó. Ta thường gặp một số dạng như sau:
Dạng 1: Tìm m để hàm số \(y = f\left( x \right)\) đạt cực đại hoặc cực tiểu tại \({x_0}\)
Phương pháp: ta sử dụng điều kiện sau:
- Nếu
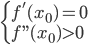 thì hàm số đạt cực tiểu tại
thì hàm số đạt cực tiểu tại 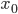 .
. - Nếu
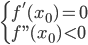 thì hàm số đạt cực đại tại
thì hàm số đạt cực đại tại 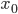 .
.
Ví dụ 1: Tìm m để hàm số 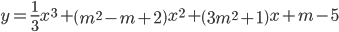 đạt cực tiểu tại x = -2.
đạt cực tiểu tại x = -2.
Giải
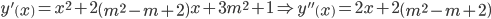
Để hàm số đạt cực tiểu tại x = -2 thì điều kiện cần là 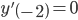 :
:
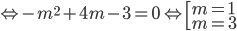
Với 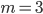 thì
thì 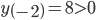 0" />
nên hàm số đạt cực tiểu tại
0" />
nên hàm số đạt cực tiểu tại 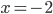 . Vậy
. Vậy 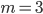 thỏa yêu cầu
thỏa yêu cầu
Với 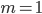 thì
thì 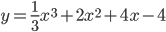 . Sử dụng bảng biến thiên ta thấy hàm số không có cực trị nên
. Sử dụng bảng biến thiên ta thấy hàm số không có cực trị nên 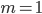 không thỏa yêu cầu.
không thỏa yêu cầu.
Vậy với m = 3 thì hàm số đạt cực tiểu tại x = -2.
Lưu ý: Với 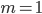 thì
thì 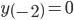 nên ta không thể kết luận mà phải sử dụng đến bảng biến thiên.
nên ta không thể kết luận mà phải sử dụng đến bảng biến thiên.
Dạng 2: Tìm m để hàm số 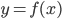 có cực trị hoặc không có cực trị.
có cực trị hoặc không có cực trị.
Đối với dạng toán này, ta thường chú ý đến 2 dạng hàm số chính:
1. Hàm số bậc 3: 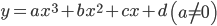
- Hàm số không có cực trị
 phương trình
phương trình 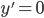 vô nghiệm hoặc nghiệm kép
vô nghiệm hoặc nghiệm kép 
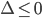 .
. - Hàm số có hai cực trị
 phương trình
phương trình 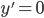 có hai nghiệm phân biệt
có hai nghiệm phân biệt 
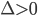
2. Hàm số bậc 4 trùng phương: 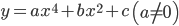
- Hàm số có 1 cực trị
 phương trình
phương trình 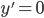 có một nghiệm duy nhất
có một nghiệm duy nhất  a.b>0.
a.b>0. - Hàm số có 3 cực trị
 phương trình
phương trình 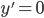 có ba nghiệm
có ba nghiệm  a.b<0.
a.b<0.
Ví dụ 2: Cho hàm số 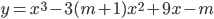 , với m là tham số thực. Xác định m để hàm số đã cho có hai cực trị.
, với m là tham số thực. Xác định m để hàm số đã cho có hai cực trị.
Giải
Ta có: 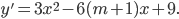
Để hàm số có hai cực trị thì phương trình y' = 0 phải có hai nghiệm phân biệt.
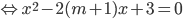 có hai nghiệm phân biệt.
có hai nghiệm phân biệt.
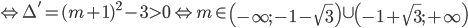
Ví dụ 3: Cho hàm số 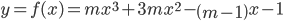 , m là tham số. Xác định các giá trị của m để hàm số không có cực trị.
, m là tham số. Xác định các giá trị của m để hàm số không có cực trị.
Giải
Với m = 0 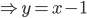
 nên hàm số không có cực trị.
nên hàm số không có cực trị.
Với 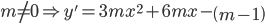
Hàm số không có cực trị khi và chỉ khi phương trình y' = 0 vô nghiệm hoặc có nghiệm kép.
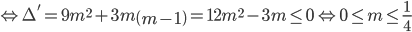
Vậy với 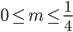 thì hàm số không có cực trị.
thì hàm số không có cực trị.
Dạng 3: Tìm tham số m để hàm số có cực trị thỏa mãn yêu cầu.
Đây là dạng bài tập nâng cao ta thường gặp trong các đề thi đại học, cao đẳng. Để làm được dạng toán này, trước tiên ta cần nắm được phương pháp giải các dạng toán đã nêu bên trên, đồng thời phải kết hợp với một số kiến thức khác về hình học, dãy số...
Ví dụ 4: Cho hàm số 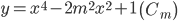 . Tìm m dể hàm số có ba điểm cực trị là ba đỉnh của một tam giác vuông cân.
. Tìm m dể hàm số có ba điểm cực trị là ba đỉnh của một tam giác vuông cân.
Giải
Trước tiên ta áp dụng phương pháp ở dạng 2 tìm m để hàm số có 3 cực trị.
Ta có: 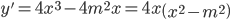
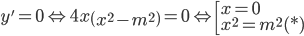
Để hàm số có 3 cực trị thì phương trình y' = 0 phải có 3 nghiệm phân biệt.
 Phương trình (*) phải có 2 nghiệm phân biệt khác o
Phương trình (*) phải có 2 nghiệm phân biệt khác o 
Vậy với 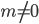 thì hàm số có 3 cực trị.
thì hàm số có 3 cực trị.
Bây giờ ta sẽ tìm m để 3 cực trị này tạo thành 3 đỉnh của một tam giác vuông cân.
Ta có: với 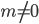 thì
thì 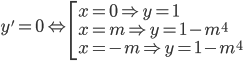
Gọi 3 điểm cực trị lần lượt là: 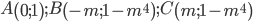
Theo tính chất của hàm số bậc 4 trùng phương thì tam giác ABC cân tại A nên để ABC vuông cân thì AB vuông góc với AC
\(\overrightarrow{AB}.\overrightarrow{AC}=0\)
<=> m = 0 (loại) hoặc m =-1; m= 1 ( thỏa mãn)
Vậy với m = -1 và m = 1 thì thỏa mãn yêu cầu bài toán.
Trên đây là ba dạng toán cực trị hàm số mà chúng ta thường gặp. Trong đó dạng 1 và 2 là các dạng cơ bản chúng ta phải nắm vững trước khi tìm hiểu đến dạng 3.









