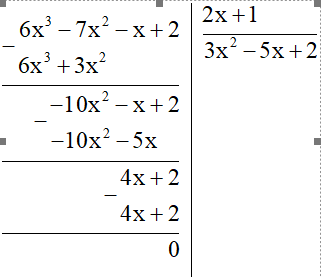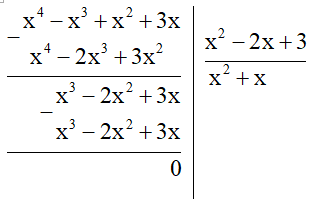ÔN TẬP VỀ ĐA THỨC – PHẦN 2

ÔN TẬP VỀ ĐA THỨC – PHẦN 2

Bài 1: Làm tính nhân:

a, 3x(x² – 7x + 9)

b, 2/5 xy(x²y – 5x + 10y)

Lời giải:

a, 3x(x² – 7x + 9) = 3x³ – 21x² + 27x

b, 2/5 xy(x²y – 5x + 10y) = 2/5 x³y² – 2x²y + 4xy²

Bài 2: Làm tính nhân:

a, (x² – 1)(x² + 2x)

b, (x + 3y)(x² – 2xy + y)

c, (2x – 1)(3x + 2)(3 – x)

Lời giải:

a, (x² – 1)(x² + 2x)

= x⁴ + 2x³ – x² – 2x

b, (x + 3y)(x² – 2xy + y)

= x³ – 2x²y + xy + 3x²y – 6xy² + 3y²

= x³ + x²y + xy – 6xy² + 3y²

c, (2x – 1)(3x + 2)(3 – x)

= (6x² + 4x – 3x – 2)(3 – x)

= (6x² + x – 2)(3 – x)

= 18x² – 6x³ + 3x – x² – 6 + 2x

= 17x² – 6x³ + 5x – 6

Bài 3: Tính nhanh giá trị của mỗi biểu thức sau:

a, 1,6² + 4.0,8.3,4 + 3,4²

b, 3⁴.5⁴ – (15² + 1)(15² – 1)

c, x⁴ – 12x³ + 12x² – 12x + 111 tại x = 11

Lời giải:

a, 1,6² + 4.0,8.3,4 + 3,4²

= 1,6² + 2.1,6.3,4 + 3,4²

= (1,6 + 3,4)² = 5² = 25

b, 3^4.5⁴ – (15² + 1)(15² – 1)

= (3.5)⁴ – (15⁴ – 1)

= 15⁴ - 15⁴ + 1 = 1

c, Với x = 11, ta có: 12 = x + 1

Suy ra: x⁴ – 12x³ + 12x² – 12x + 111

= x⁴ – (x + 1)x³ + (x + 1)x² – (x + 1)x + 111

= x⁴ - x⁴ - x³ + x³ + x² - x² – x + 111 = - x + 111

Thay x = 11 vào biểu thức ta được: - x + 111 = - 11 + 111 = 100

Bài 4: Rút gọn biểu thức:

a, (6x + 1)² + (6x – 1)² – 2(1 + 6x)(6x – 1)

b, 3(2² + 1)(2⁴ + 1)(2⁸ + 1)(2¹⁶ + 1)

Lời giải:

a, (6x + 1)² + (6x – 1)² – 2(1 + 6x)(6x – 1)

= (6x + 1)² – 2(1 + 6x)(6x – 1) + (6x – 1)²

= [(6x + 1) – (6x – 1)]²

= (6x + 1 – 6x + 1)² = 2² = 4

b, 3(2² + 1)(2⁴ + 1)(2⁸ + 1)(21⁶ + 1)

= (2² – 1)(2² + 1)(2⁴ + 1)(2⁸ + 1)(2¹⁶ + 1)

= (2⁴ - 1)(2⁴ + 1)(2⁸ + 1)(2¹⁶ + 1)

= (2⁸ - 1)(2⁸ + 1)(2¹⁶ + 1)

= (2¹⁶ - 1)(2¹⁶ + 1)

= 2³² – 1

Bài 5: Phân tích đa thức thành nhân tử:

a, x³ – 3x² – 4x + 12

b, x⁴ – 5x² + 4

c, (x + y + z)³ – x³ – y³ – z³

Lời giải:

a, x³ – 3x² – 4x + 12

= (x³ – 3x² ) – (4x – 12)

= x²(x – 3) – 4(x – 3)

= (x – 3)(x² – 4)

= (x – 3)(x + 2)(x – 2)

b, x⁴ – 5x² + 4

= x⁴ – 4x² - x² + 4

= (x⁴ – 4x² ) – (x² - 4)

Bài 6: Làm tính chia:

a) (6x³– 7x²– x + 2) : (2x + 1)

b) (x⁴– x³+ x² + 3x) : (x² – 2x + 3)

c) (x²– y²+ 6x + 9) : (x + y + 3)

Lời giải:

a)

b)

c) (x²– y²+ 6x + 9) : (x + y + 3)

= (x² + 6x + 9 – y²) : (x + y + 3)

= [(x² + 2.x.3 + 3²) – y²] : (x + y + 3)

= [(x + 3)² – y²] : (x + y + 3)

= (x + 3 + y)(x + 3 – y) : (x + y + 3)

= x + 3 – y = x – y + 3

Bài 7: Tìm x, biết:

a) \(\frac{2}{3}x({x^2} - 4) = 0\)

b) (x + 2)²– (x – 2)(x + 2) = 0

c) x + 2√2 x²+ 2x³= 0

Lời giải

\(\begin{array}{l}a)\frac{2}{3}x({x^2} - 4) = 0\\ \Leftrightarrow \frac{2}{3}x({x^2} - {2^2}) = 0\\ \Leftrightarrow \frac{2}{3}x(x + 2)(x - 2) = 0\end{array}\)

Hoặc x = 0

Hoặc x – 2 = 0 => x = 2

Hoặc x + 2 = 0 => x = - 2

Vậy x = 0; x = - 2; x = 2

b) (x + 2)²– (x – 2)(x + 2) = 0

⇔ (x + 2)[(x + 2) – (x – 2)] = 0

⇔ (x + 2)(x + 2 – x + 2) = 0

⇔ (x + 2).4 = 0

⇔ x + 2 = 0

=> x = - 2

\(\begin{array}{l}c)x + 2\sqrt 2 {x^2} + 2{x^3} = 0\\ \Leftrightarrow x(1 + 2\sqrt 2 x + 2{x^2}) = 0\\ \Leftrightarrow x{\rm{[}}1 + 2\sqrt 2 x + {(\sqrt 2 x)^2}{\rm{]}} = 0\\ \Leftrightarrow x{(1 + \sqrt 2 x)^2} = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  - \frac{1}{{\sqrt 2 }}\end{array} \right.\end{array}\)

Bài 8: Chứng minh:

a) x²– 2xy + y²+ 1 > 0 với mọi số thực x và y.

b) x – x²– 1 < 0 với mọi số thực x.

Lời giải:

a) Ta có:

x² – 2xy + y² + 1

= (x² – 2xy + y²) + 1

= (x – y)² + 1 > 0 do (x – y)² ≥ 0 với mọi x, y (đpcm).

b) Ta có:

x – x² – 1 = - (x² – x + 1)