Lý thuyết hàm số lượng giác
Cập nhật lúc: 11:55 04-08-2017 Mục tin: LỚP 11
Xem thêm:
LÝ THUYẾT HÀM SỐ LƯỢNG GIÁC
1. Hàm tuần hoàn
Hàm số f(x) xác định trên tập hợp D gọi là tuần hoàn nếu tồn tại một số dương T sao cho với mọi \(\tiny $$x \in D$$\) ta có:
\(x - T \in D\) và \(x + T \in D\) (1)
\(f\left( {x + T} \right) = f\left( x \right)\,\,\left( 2 \right)\)
Số nhỏ nhất (nếu có) trong các số T có các tính chất trên gọi là chu kỳ cơ sở của hàm số tuần hoàn f(x).
Chú ý: (Các dấu hiệu để nhận biết hàm số f(x) không phải là hàm tuần hoàn)
Hàm số f(x) không phai là hàm tuần hoàn khi một trong các điều kiện sau bị vi phạm.
1. Tập xác định của hàm số là tập hữu hạn
2. Tồn tại số a sao cho hàm số không xác định với x > a hoặc x < a
3. Phương trình f(x) = k có nghiệm nhưng số nghiệm hữu hạn.
4. Phương trình f(x) = k có vô số nghiệm sắp thứ tự \(...{x_n} < {x_{n + 1}} < ...\) mà \(\left| {{x_n} - {x_{n + 1}}} \right| \to 0\) hay \(\infty \).
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
-
Tìm tập xác định của hàm số lượng giác ( có lời giải chi tiết)(09/08)
Bài toán tìm tập xác định của hàm số lương giác là dạng toán đầu tiên của phần hàm số lượng giác môn Toán lớp 11.
-
Kiến thức cơ bản cần nắm vững hàm số lượng giác(09/08)
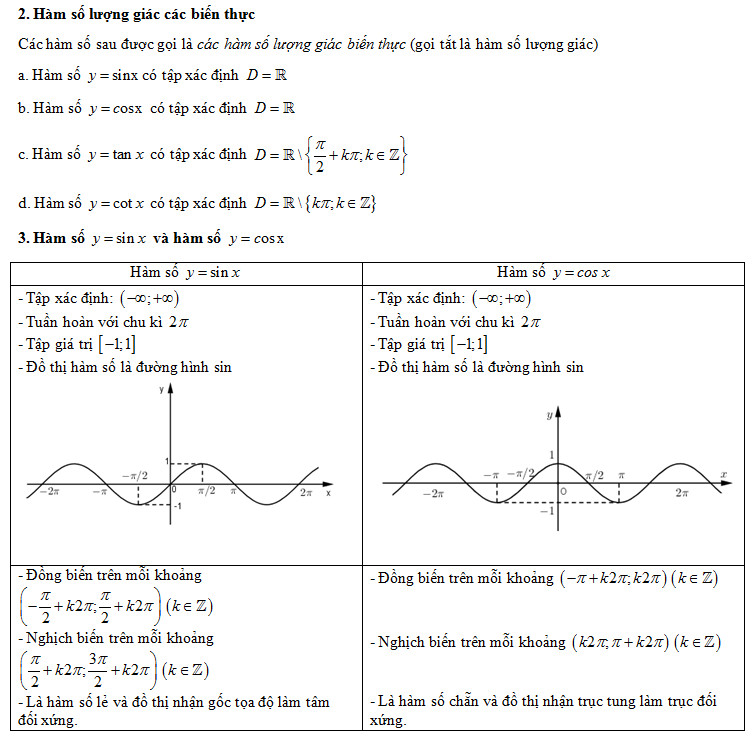
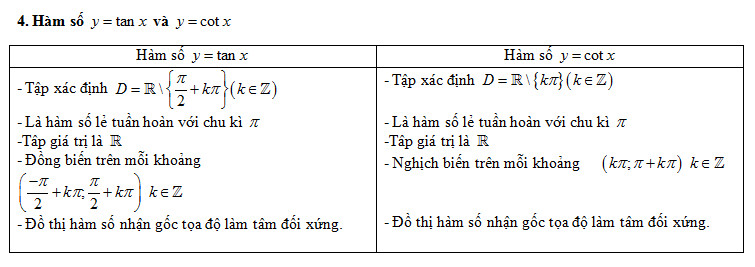
Sau đây ta sẽ tìm hiểu về các hàm số lượng giác cơ bản, thường gặp trong chương trình Toán 11 như hàm y = sinx, y = cos x, y = tan x, y = cot x.
-
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số lượng giác (có lời giải chi tiết)(09/08)
Tìm giá trị lớn nhất và nhỏ nhất của hàm số lượng giác là một bài toán thường gặp. Học sinh thường nghĩ bài toán này khó và phải vận dụng nhiều bất đẳng thức. Tuy nhiên với tính chất cơ bản của các hàm số lượng giác thì bài toán tìm giá trị lớn nhất và nhỏ nhất của các hàm số lượng giác trở nên đơn giản hơn.
-
Xét tính chẵn lẻ của hàm số lượng giác(09/08)
Bài viết trình bày phương pháp xét tính chẵn lẻ của hàm số lượng giác nói riêng và các hàm số nói chung.
-
Xét tính tuần hoàn của các hàm số lượng giác(08/08)
Trong chương trình THPT, kiến thức về hàm số tuần hoàn (HSTH) được đề cập rất ít, chủ yếu khi học sinh được học về các tính chất của các hàm số lượng giác ở lớp 11. Tuy nhiên trong các kì thi học sinh giỏi, vẫn thường hay xuất hiện những bài toán liên quan đến nội dung này.
-
Tập xác định của hàm số lượng giác(04/08)
Tìm tập xác định của các hàm số lượng giác là một bước làm quan trọng trong quá trình giải các phương trình lượng giác. Bài tập (có lời giải chi tiết) giúp học sinh tránh nhầm lẫn trong quá trình tìm tập xác định của các hàm số lượng giác.
-
55 Câu Trắc Nghiệm Các Hàm Số Lượng Giác(04/08)
55 câu trắc nghiệm các hàm số lượng giác tổng hợp đầy đủ tất cả các dạng bài về hàm số lượng giác và đồ thị hàm số lượng giác giúp nắm chắc tất cả các kiến thức ban đầu về chương 1: Hàm số lượng giác và các phương trình lượng giác.

