Luyện tập hình thang

LUYỆN TẬP HÌNH THANG

Câu 1: Tính các góc của hình thang ABCD (AB // CD), biết rằng A = 3D, B - C = 30^o.

Lời giải:

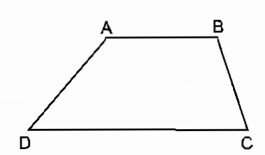
Ta có: AB // CD ⇒ A + D = 180^o (hai góc trong cùng phía)

Ta có: A = 3D (gt)

⇒ 3D + D = 180^o ⇒ D = 45^o ⇒ A = 3.45^o = 135^o

B + C = 180^o (hai góc trong cùng phía)

B - C = 30^o (gt)

⇒ 2B = 210^o ⇒ B = 105^o

C = B - 30^o = 105^o – 30^o = 75^o

Câu 2: Tứ giác ABCD có BC = CD và DB là tia phân giác của góc D. chứng minh rằng ABCD là hình thang.

Lời giải:

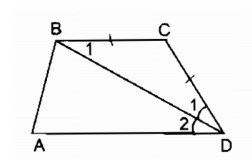
ΔBCD có BC = CD (gt) nên ΔBCD cân tại C.

⇒ ∠B1= ∠D1(tính chất tam giác cân)

Mà ∠D1= ∠D2(gt)

Suy ra: ∠B1= ∠D2

Do đó: BC // AD (vì có cặp góc ở vị trí so le trong bằng nhau)

Vậy ABCD là hình thang.

Câu 3: Xem các hình dưới và cho biết:

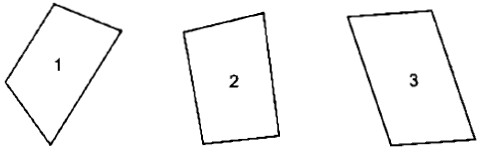
a, Tứ giác ở hình (1) chỉ có mấy cặp cạnh đối song song?

b, Tứ giác ở hình (3) có mấy cặp cạnh đối song song?

c, Tứ giác ở hình nào là hình thang?

Lời giải:

a, Tứ giác ở hình (1) chỉ có 1 cặp cạnh đối song song.

b, Tứ giác ở hình (3) có hai cặp cạnh đối song song.

c, Tứ giác ở hình (1) và hình (3) là hình thang.

Câu 4: Tính các góc B và D của hình thang ABCD, biết rằng: A = 60^o, C = 130^o

Lời giải:

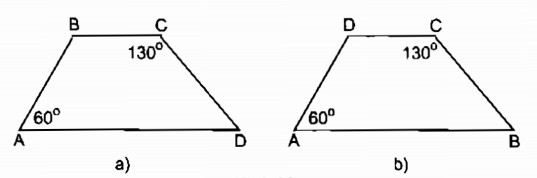
Trong hình thang ABCD, ta có A và C là hai góc đối nhau.

a, Trường hợp A và B là 2 góc kề với cạnh bên.

⇒ AB // CD

A + B = 180^o (hai góc trong cùng phía bù nhau)

⇒ B = 180^o - A = 180^o – 60^o = 120^o

C + D = 180^o (hai góc trong cùng phía bù nhau)

⇒ D = 180^o - C = 180^o – 130^o = 50^o

b, Trường hợp A và D là 2 góc kề với cạnh bên.

⇒ AB // CD

A + D = 180^o (hai góc trong cùng phía bù nhau)

⇒ D = 180^o - A = 180^o – 60^o = 120^o

C + B = 180^o (hai góc trong cùng phía bù nhau)

⇒ B = 180^o - C = 180^o – 130^o = 50^o

Câu 5: Chứng minh rằng trong hình thang có nhiều nhất là hai góc tù, có nhiều nhất là hai góc nhọn.

Lời giải:

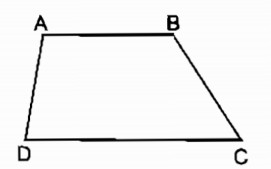
Xét hình thang ABCD có AB //CD.

Ta có:

* ∠A và ∠D là hai góc kề với cạnh bên

⇒ ∠A + ∠D = 180^o (2 góc trong cùng phía) nên trong hai góc đó có nhiều nhất 1 góc nhọn và có nhiều nhất là 1 góc tù.

* ∠B và ∠C là hai góc kề với cạnh bên

⇒ ∠B + ∠C = 180^o (2 góc trong cùng phía) nên trong hai góc đó có nhiều nhất 1 góc nhọn và có nhiều nhất là 1 góc tù.

Vậy trong bốn góc là A, B, C, D có nhiều nhất là hai góc tù và có nhiều nhất là hai góc nhọn.

Câu 6: Chứng minh rằng trong hình thang các tia phân giác của hai góc kề với một cạnh bên vuông góc với nhau.

Lời giải:

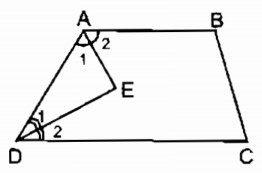
Giả sử hình thang ABCD có AB // CD

* Ta có: ∠A1= ∠A2= 12 ∠A (gt)

∠D1= ∠D2= 12 ∠D (gt)

Mà ∠A + ∠D = 180^o (2 góc trong cùng phía bù nhau)

Suy ra: ∠A1+ ∠D1= 12 (∠A1+ ∠D1) = 90^o

* Trong ΔAED, ta có:

(AED) + ∠A1+ ∠D1= 180o (tổng 3 góc trong tam giác)

⇒ (AED) = 180^o – (∠A1+ ∠D1) = 180^o - 90^o

Vậy AE ⊥ DE.

Câu 7: Cho tam giác ABC, các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC cắt các cạnh AB và AC ở D và E.

a, Tìm các hình thang trong hình vẽ.

b, Chứng minh rằng hình thang BDEC có một đáy bằng tổng hai cạnh bên.

Lời giải:

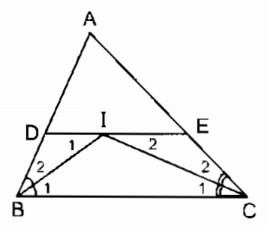
a, Đường thẳng đi qua I song song với BC cắt AB tại D và AC tại E, ta có các hình thang sau: BDEC, BDIC, BIEC

b, DE // BC (theo cách vẽ)

⇒ ∠I1= ∠B1(hai góc so le trong)

Mà ∠B1= ∠B2(gt)

Suy ra: ∠I1= ∠B2

Do đó: ΔBDI cân tại D ⇒ DI = DB (1)

Ta có: ∠I2= ∠C1(so le trong)

∠C1= ∠C2(gt)

Suy ra: ∠I1= ∠C2 do đó: ΔCEI cân tại E

⇒ IE = EC (2)

DE = DI + IE (3)

Từ (1), (2), (3) suy ra: DE = BD + CE

Câu 8: Cho tam giác ABC vuông cân tại A. Ở phía ngoài tam giác ABC, ve tam giác BCD vuông cân tại B. Tứ giác ABCD là hình gì? Vì sao?

Lời giải:

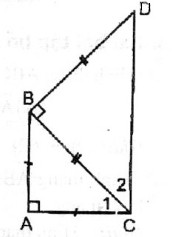
Vì ΔABC vuông cân tại A nên ∠C1= 45^o

Vì ΔBCD vuông cân tại B nên ∠C2= 45^o

∠(ACD) = ∠C1+ ∠C2= 45^o + 45^o = 90^o

⇒ AC ⊥ CD

Mà AC ⊥ AB (gt)

Suy ra: AB //CD

Vậy tứ giác ABCD là hình thang vuông.

Câu 9: Hình thang vuông ABCD có ∠A = ∠D = 90^o, AB = AD = 2cm, DC = 4cm. Tính các góc của hình thang.

Lời giải:

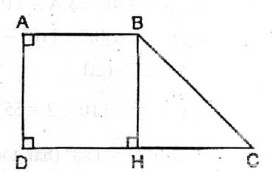
Kẻ BH ⊥ CD

Ta có: AD ⊥ CD (gt)

Suy ra: BH // AD

Hình thang ABHG có hai cạnh bên song song nên HD = AB và BH = AD

AB = AD = 2cm (gt)

⇒ BH = HD = 2cm

CH = CD – HD = 4 – 2 = 2 (cm)

Suy ra: ΔBHC vuông cân tại H ⇒ ∠C = 45o

∠B + ∠C = 180^o (2 góc trong cùng phía) ⇒ ∠B = 180^o – 45^o = 135^o

Câu 10: Chứng minh rằng tổng hai cạnh bên của hình thang lớn hơn hiệu của hai đáy.

Lời giải:

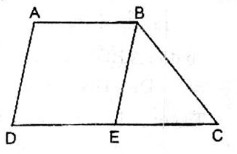
Giả sử hình thang ABCD có AB // CD

Từ B kẻ đường thẳng song song với AD cắt CD tại E.

Hình thang ABED có hai cạnh bên song song nên AB = ED và AD = BE

Ta có: CD – AB = CD – ED = EC (1)

Trong ΔBEC ta có:

BE + BC > EC (bất đẳng thức tam giác)

Mà BE = AD

Suy ra: AD + BC > EC (2)

Từ (1) và (2) suy ra: AD + BC > CD – AB