Bài tập giới hạn dãy số - có lời giải chi tiết

Loại 1: Giới hạn của dãy số hữu tỉ

Phương pháp: Xem xét bậc cao nhất của tư và mẫu. Sau đó, chia tử và mẫu cho bậc cao nhất của tử và mẫu. Hoặc cũng cóthể đặt nhân tử cao nhất của từ và mẫu để được những giới hạn cơ bản. Tính giới hạn này.

Trích dẫn: Qua 3 bài toán ở trên dạng dãy số dạng hữu tỉta rút ra nhận xét như sau.

+ Nếu bậc của tử lớn hơn bậc của mẫu thì giới hạn đó bằng + - vô cùng

+ Nếu bậc của tử bằng bậc của mẫu thì giới hạn đó bằng hệ số bậc cao nhất của tử trên hệ số bậc cao nhất của mẫu

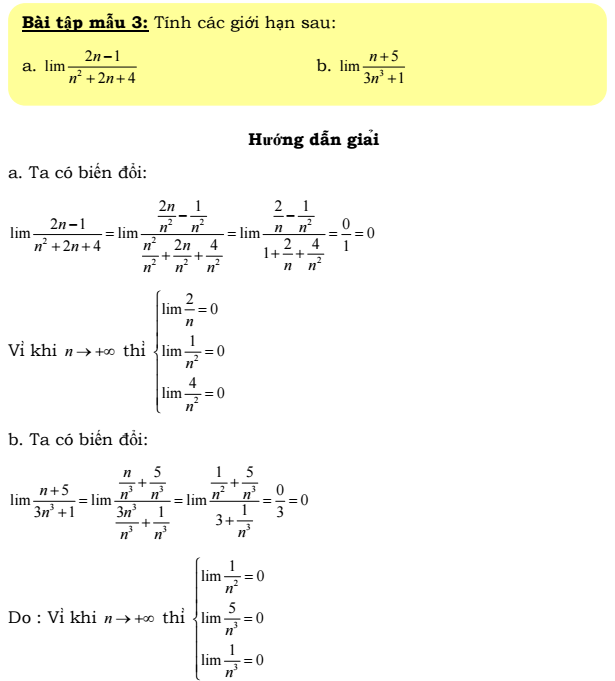
Bài tập mẫu 3: Tính các giới hạn sau:

+ Nếu bậc của tử béhơn bậc của mẫu thì giới hạn đó bằng 0.

Điều này rất cần thiết cho tất cả chúng ta giải bài toán giới hạn dạng hữu tỉ khi giải trắc nghiệm. Bởi vì một giới hạn hữu tỉ khi nhìn vào ta hoàn toàn cóthể biết được kết quả ngay lập tức. Thật vậy những bài toán sau các em hoàn toàn biết được kết quả một cách nhanh chóng và chính xác.

Thật vậy, sử dụng nhận xét đóta thực hiện nhanh các bài tập trắc nghiệm sau: