Trắc nghiệm Quan hệ vuông góc trong không gian (có đáp án)
Cập nhật lúc: 11:31 10-02-2017 Mục tin: LỚP 11
Xem thêm:
BÀI 1: VEC TƠ TRONG KHÔNG GIAN
Câu 1: Cho hình lăng trụ ABC.A'B'C', M là trung điểm của BB'. Đặt \(\overrightarrow{CA}=\overrightarrow{a}; \overrightarrow{CB}=\overrightarrow{b};\overrightarrow{AA'}=\overrightarrow{c}\) khẳng định nào sau đây đúng?
A.\(\overrightarrow{AM}=\overrightarrow{b}+\overrightarrow{c}-\frac{1}{2}\overrightarrow{a}\) B.\(\overrightarrow{AM}=\overrightarrow{a}-\overrightarrow{c}-\frac{1}{2}\overrightarrow{b}\)
C.\(\overrightarrow{AM}=\overrightarrow{a}+\overrightarrow{c}-\frac{1}{2}\overrightarrow{b}\) D. \(\overrightarrow{AM}=\overrightarrow{b}-\overrightarrow{a}+\frac{1}{2}\overrightarrow{c}\)
Câu 2: Trong không gian cho điểm O và bốn điểm A,B,C,D không th\(\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}=\overrightarrow{OC}+\frac{1}{2}\overrightarrow{OD}\)ẳng hàng. Điều kiện cần và đủ để A,B,C,D tạo thành hình bình hành là:
A.\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}\) B.\(\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}\)
C.\(\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}=\overrightarrow{OC}+\frac{1}{2}\overrightarrow{OD}\) D.\(\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OC}=\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OD}\)
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đặt \(\overrightarrow{SA}=\overrightarrow{a}; \overrightarrow{SB}=\overrightarrow{b};\overrightarrow{SC}=\overrightarrow{c}=\overrightarrow{SD}=\overrightarrow{d}\)
A.\(\overrightarrow{a}+\overrightarrow{c}=\overrightarrow{b}+\overrightarrow{d}\) B.\(\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{c}+\overrightarrow{d}\)
C.\(\overrightarrow{a}+\overrightarrow{d}=\overrightarrow{b}+\overrightarrow{c}\) D.\(\overrightarrow{a}+\overrightarrow{c}+\overrightarrow{b}+\overrightarrow{d}=\overrightarrow{0}\)












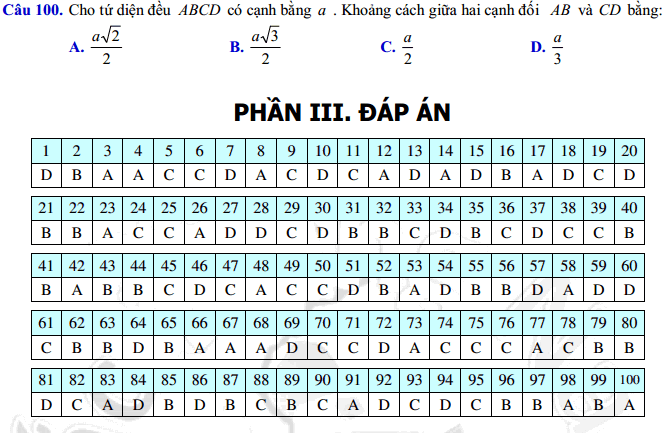
Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
-
Lý thuyết - Bài tập tính khoảng cách trong không gian lớp 11(23/02)
Loại toán tính khoảng cách trong hình học không gian là một trong những loại toán hay, đòi hỏi tư duy đối với học sinh THPT và thường gặp trong các đề thi đại học. Khi gặp loại toán này học sinh thường rất lúng túng không biết hướng giải quyết.Tài liệu nhằm giúp các em có thêm kiến thức, phát triển năng lực tư duy sáng tạo và gợi cho các em hướng giải quyết tốt khi gặp loại toán này.
-
Trắc nghiệm quan hệ vuông góc trong không gian(20/01)
Tài liệu gồm 42 câu trắc nghiệm có đáp án, tập trung vào kiểm tra các tính chất của chương quan hệ vuông góc trong không gian, giúp các em hiểu sâu lý thuyết hơn, là cơ sở làm bài tập vận dụng được tốt.
-
Lý thuyết - phương pháp - bài tập Quan hệ vuông góc trong không gian (chi tiết, đầy đủ)(20/01)
Tài liệu gồm 25 trang đầy đủ lý thuyết và bài tập, được phân dạng rõ ràng có bài tập áp dụng, lời giải chi tiết giúp các em ôn tập đạt kết quả cao.

