Tổng hợp chuyên đề quan hệ vuông góc trong không gian
Cập nhật lúc: 16:07 23-07-2015 Mục tin: LỚP 12
Xem thêm:
I. Hai đường thẳng vuông góc với nhau
A. Phương pháp chứng minh:
C1 : Dùng các quan hệ vuông góc đã biết trong mặt phẳng
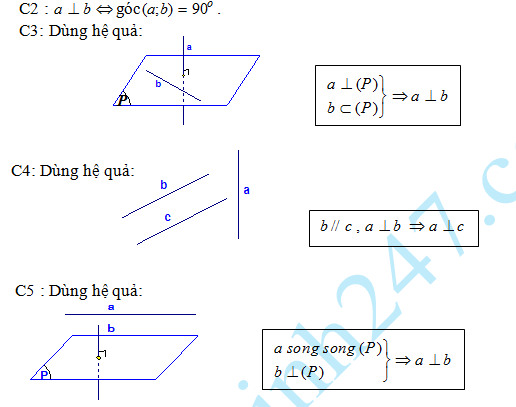
C6 : Sử dụng định lí ba đường vuông góc.
C7: Dùng hệ quả: Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì vuông góc với cạnh còn lại của tam giác









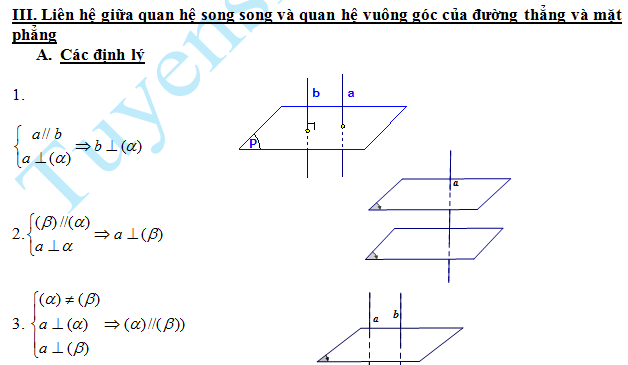


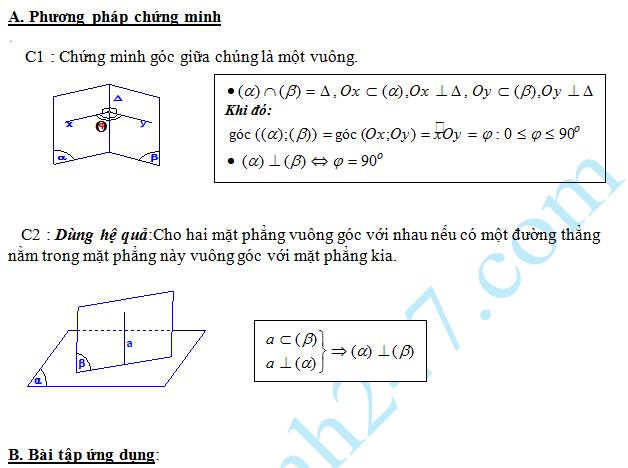
Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
-
Trắc nghiệm Quan hệ vuông góc trong không gian (có đáp án)(10/02)
Tổng hợp 100 câu trắc nghiệm chương quan hệ vuông góc trong không gian phân theo từng dạng cụ thể có đáp án giúp các em ôn tập chuẩn bị tốt cho bài kiểm tra cuối chương.
-
Tâm pháp hình học không gian - cực hay - cực hiểu(16/03)
Tài liệu dưới đây gồm toàn bộ những phương pháp giải hình học không gian theo từng trường hợp cụ thể mà học sinh phải gặp phải trong các đề thi, khi biết được cách làm từ gốc của các bài toán phức tạp như thế nào thì chắc chắn sẽ giải quyết cực đơn giản những bài toán ta đang gặp phải. Tài liệu này rất hữu ích cho 2 đối tượng học sinh lớp 11 và học sinh lớp 12 luyện thi đại học.
-
Các quan hệ vuông góc trong không gian(14/07)
Tài liệu bày sẽ chia sẻ cho các em về các quan hệ vuông góc trong không gian như quan hệ vuông góc giữa đường thẳng với mặt phẳng, quan hệ giữa mặt phẳng với mặt phẳng, và giữa các đường thẳng với nhau. Hơn nữa tài liệu này còn đưa ra các phương pháp hay và các ví dụ kèm lời giải chi tiết học sinh có thể vận dụng tốt khi gặp loại bài tập này.

