Phương pháp tìm giao tuyến của hai mặt phẳng và một số bài tập áp dụng có lời giải chi tiết.
Cập nhật lúc: 15:00 03-08-2017 Mục tin: LỚP 11
Xem thêm:
GIAO TUYẾN CỦA HAI MẶT PHẲNG
I. Các phương pháp:
Phương pháp 1
Cơ sở của phương pháp tìm giao tuyến của hai mặt phẳng \((\alpha )\) và \( (\beta )\) cần thực hiện:
- Bước 1: Tìm hai điểm chung A và B của \( \alpha \) và \( (\beta )\) .
- Bước 2: Đường thẳng AB là giao tuyến cần tìm \( \left( {AB = (\alpha ) \cap (\beta )} \right) \) .
Chú ý : Để tìm chung của \((\alpha )\) và \( (\beta )\) thường tìm 2 đường thẳng đồng phẳng lần
lượt nằm trong hai mp giao điểm nếu có của hai đường thẳng này là điểm chung của hai mặt phẳng.
Phương pháp 2
Tương tự phương pháp 1 khi chỉ tìm ngay được 1 điểm chung \(S\).
Lúc này ta có hai trường hợp:
- TH1: Hai mặt phẳng \((\alpha )\) và \( (\beta )\) theo thứ tự chứa hai đường thẳng \(d_{1}\) và \(d_{2}\) mà \(d_1 \cap d_2 = I\).
\(\Rightarrow SI\) là giao tuyến cần tìm (tức là \( (\alpha ) \cap (\beta))= SI\))
- TH2: Hai mặt phẳng \((\alpha )\) và \( (\beta )\) lần lượt chứa hai đường thẳng \(d_{1}\) và \(d_{2}\) mà \(d_1 // d_2 \).
Dựng \( xSy \) song song với \(d_1\) hoặc \(d_2\).
\(\Rightarrow xSy\) là giao tuyến cần tìm. (tức là \( (\alpha ) \cap (\beta ))= xSy\)).
II. Các bài tập tự luận có lời giải chi tiết:
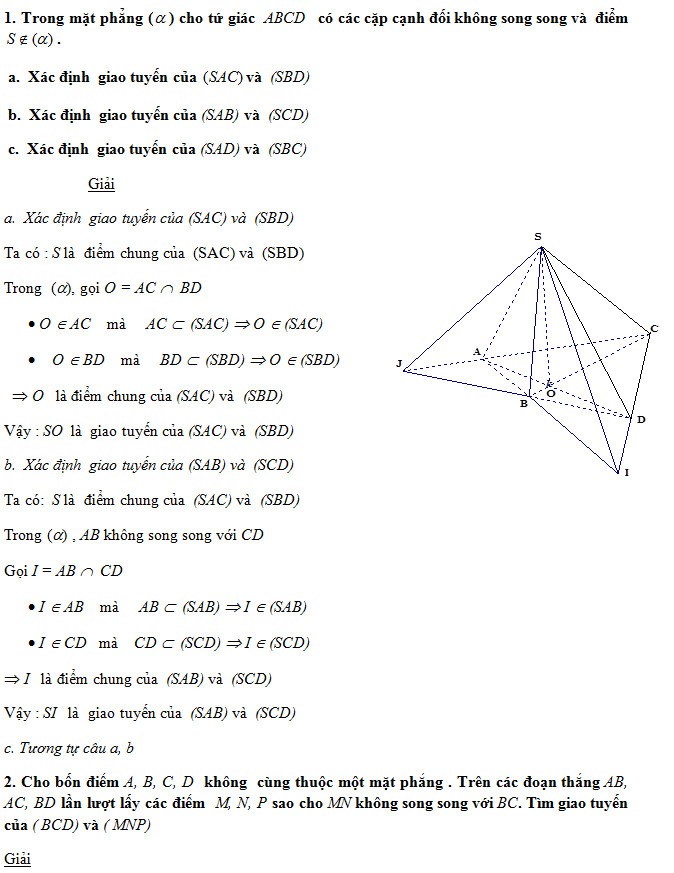
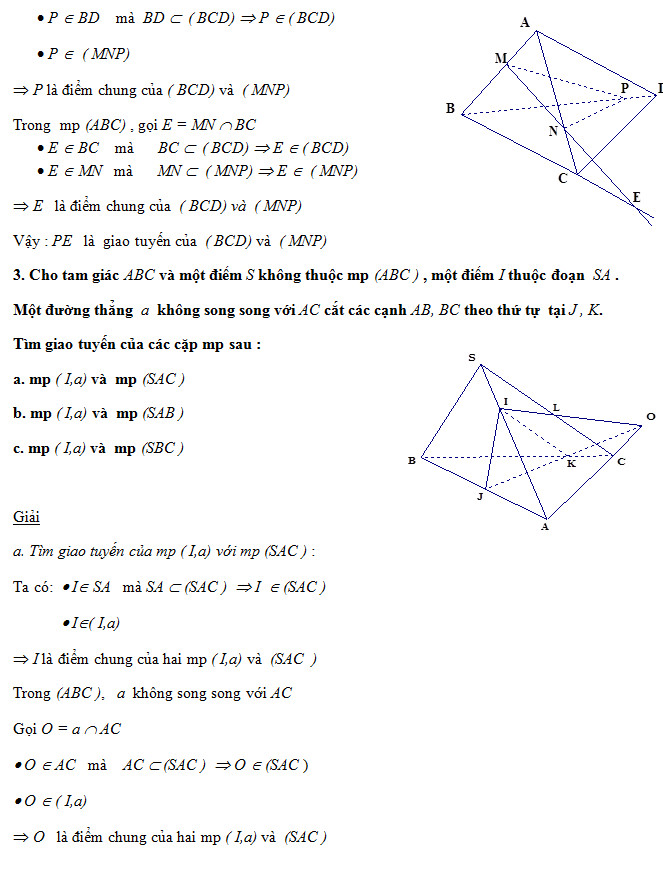
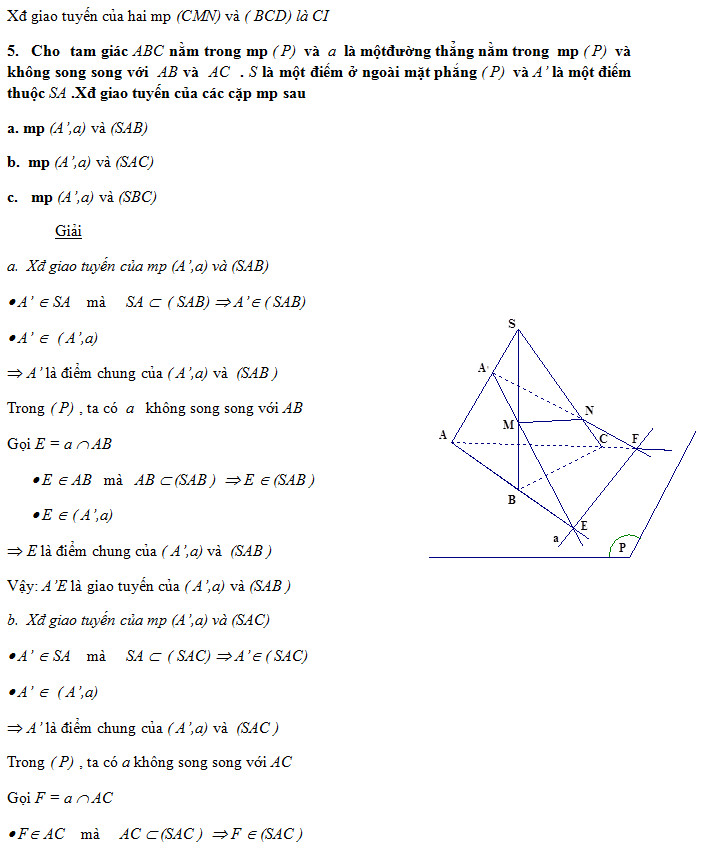
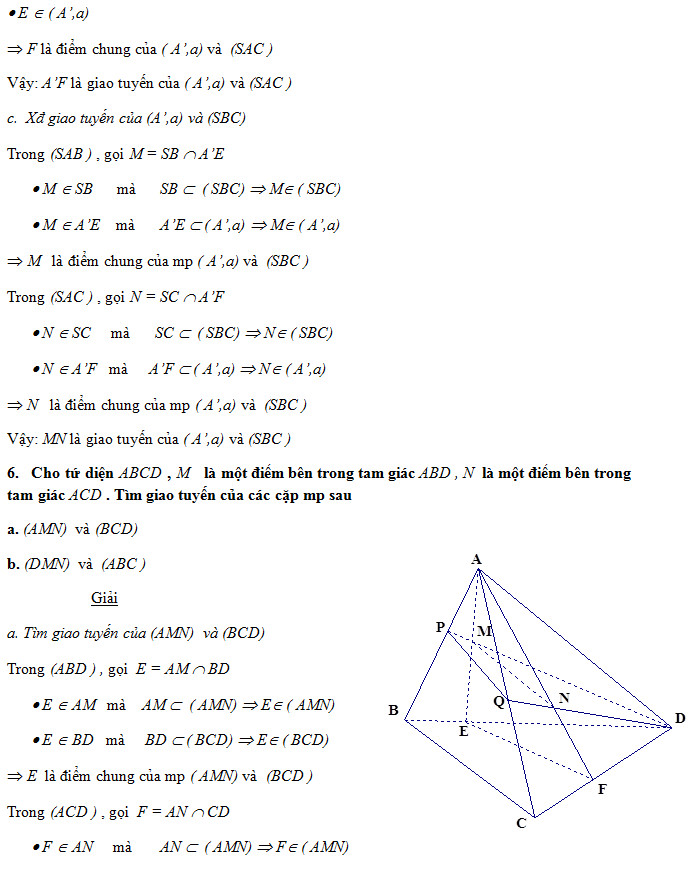
III. Các bài tập tự luyện:
Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:
Tham Gia Group Dành Cho Lớp 11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
-
50 bài tập trắc nghiệm quan hệ song song(26/10)
Sưu tầm 50 bài tập trắc nghiệm quan hệ song song - Nguyễn Quốc Tuấn
-
Phương pháp tìm giao điểm của đường thẳng và mặt phẳng - Một số bài tập áp dụng có lời giải chi tiết.(08/08)
Bài viết này giúp các em nắm chắc kiến thức cơ bản của hình học không gian để có thể làm các bài tập về hình học không gian.
