Giải phương trình mũ bằng phương pháp đặt ẩn phụ

GIẢI PHƯƠNG TRÌNH MŨ BẰNG PHƯƠNG PHÁP ĐẶT ẨN PHỤ

Phương pháp 

Ví dụ 3: Giải các phương trình sau:

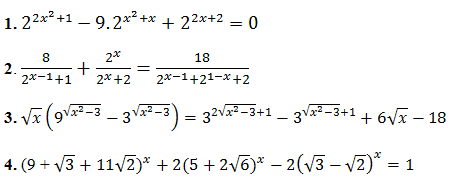
Lời giải:

1. Chia cả 2 vế của phương trình cho \(2^{2x+2}\neq 0\) ta được:

+) TH1: t= 4 <=> \(2^{x^{2}-x}=4 \Leftrightarrow x^{2}-x = 2\) <=> x = -1 ; x = 2

+) TH2: t = 1/2 <=> \(2^{x^{2}-x}=2^{-1}\Leftrightarrow x^{2}-x=-1\) <=> phương trình vô nghiệm

Vậy, phương trình đã cho có 2 nghiệm: x = -1; x = 2.

Chú ý: Để ý bài toán cho không có tham số nên ta sử dụng điều kiện cho ẩn phụ chỉ là t >0 và nếu t= 1/2 vô nghiệm. Nếu bài toán có chứa tham số thì điều kiện đúng của t:

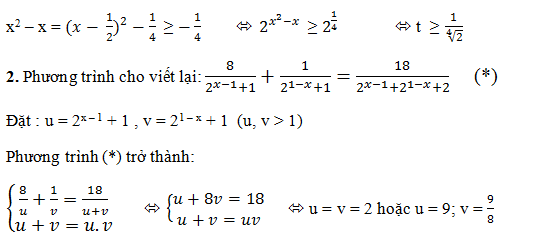
+) Với u = v = 2, ta được: