Bài giảng: Các bài toán về vectơ - Thầy Nguyễn Công Nguyên
Cập nhật lúc: 16:05 06-09-2018 Mục tin: LỚP 10
Xem thêm:
I. Các khái niệm
1) Định nghĩa
|
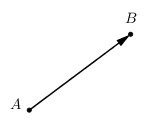
* Vectơ là một đoạn thẳng có hướng. Kí hiệu: \(\overrightarrow {AB} \) * A – gốc; B – ngọn. \(A \equiv B \Rightarrow \overrightarrow 0 \) * AB – độ dài vectơ, \(\left| {\overrightarrow {AB} } \right| = AB\) |
|
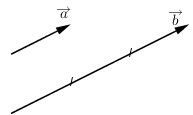
2) Hai vectơ cùng phương: \(\overrightarrow a //\overrightarrow b \Leftrightarrow \left[ \begin{array}{l}gia\,\,\overrightarrow a //gia\,\,\overrightarrow b \\gia\,\,\overrightarrow a \equiv gia\,\,\overrightarrow b \end{array} \right.\)
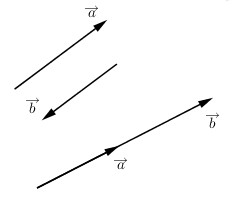
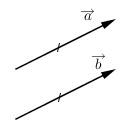
3) Hai vectơ bằng nhau: \(\overrightarrow a = \overrightarrow b \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow a \nearrow \nearrow \overrightarrow b \\\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right|\end{array} \right.\)
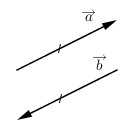
4) Hai vectơ đối: \(\overrightarrow a = - \overrightarrow b \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow a \nearrow \swarrow \overrightarrow b \\\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right|\end{array} \right.\)
III. Các bài toán về vectơ
1) Cộng
* Quy tắc ba điểm: A, B, C bất kì.
* Mở rộng: \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DE} = \overrightarrow {AE} \)
* Chú ý: \(\overrightarrow a + \left( { - \overrightarrow a } \right) = \overrightarrow 0 \)
2) Quy tắc hình bình hành
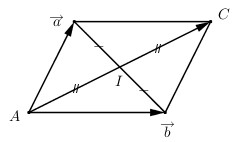
3) Nhận vectơ với số \(k \ne 0\)
|
\(k\overrightarrow a = \overrightarrow b \) khi và chỉ khi: * \(\left| {\overrightarrow b } \right| = k\left| {\overrightarrow a } \right|\) * \(\overrightarrow b \) cùng chiều với \(\overrightarrow a \Leftrightarrow k > 0\) \(\overrightarrow b \) ngược chiều với \(\overrightarrow a \Leftrightarrow k < 0\) |
|
4) Tích vô hướng của 2 vectơ
*
* \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = 0\)
IV. Các dạng toán về vectơ
1) Dạng 1: Chứng minh hệ thức vectơ
* Phương pháp 1:
* Phương pháp 2: Chứng minh \(\left. \begin{array}{l}VT = P\\VP = P\end{array} \right\} \Rightarrow VT = VP\)
* Công thức:
1. \(\overrightarrow {AB} + \overrightarrow {BA} = \overrightarrow 0 \)
2. \(\overrightarrow {AB} = \overrightarrow {AM} + \overrightarrow {MB} \)
3. Quy tắc hình bình hành.
V. Bài tập
|
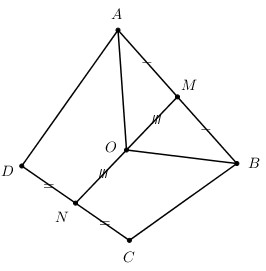
Bài 1: Cho tứ giác ABCD, M, N là trung điểm AB, CD. Chứng minh \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MN} \) Giải: * Ta có: \(\begin{array}{l}\overrightarrow {AC} = \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {NC} \,\,\,\left( 1 \right)\\\overrightarrow {BD} = \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {ND} \,\,\,\,\left( 2 \right)\\*\,\,\left( 1 \right) + \left( 2 \right) \Rightarrow \overrightarrow {AC} + \overrightarrow {BD} = \left( {\overrightarrow {AM} + \overrightarrow {BM} } \right) + 2\overrightarrow {MN} + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow 0 + 2\overrightarrow {MN} + \overrightarrow 0 = 2\overrightarrow {MN} \,\,\left( {dpcm} \right)\end{array}\) |
|
Bài 2: \(\Delta ABC\) có 3 trung tuyến AM, BN, CP. Chưng minh \(\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} = \overrightarrow 0 \)
Giải:
|
* Theo quy tắc hình bình hành có: \(\begin{array}{l}\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\,\,\left( 1 \right)\\\overrightarrow {BN} = \frac{1}{2}\left( {\overrightarrow {BA} + \overrightarrow {BC} } \right)\,\,\,\,\left( 2 \right)\\\overrightarrow {CP} = \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CB} } \right)\,\,\,\,\,\,\left( 3 \right)\\\left( 1 \right) + \left( 2 \right) + \left( 3 \right) \Rightarrow VT = \frac{1}{2}\left[ {\left( {\overrightarrow {AB} + \overrightarrow {BA} } \right) + \left( {\overrightarrow {AC} + \overrightarrow {CA} } \right) + \left( {\overrightarrow {BC} + \overrightarrow {CB} } \right)} \right]\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{2}\left( {\overrightarrow 0 + \overrightarrow 0 + \overrightarrow 0 } \right) = \overrightarrow 0 = VP\end{array}\) |
|
Bài 3: Cho tam giác ABC và điểm M bất kì. G là trọng tâm tam giác ABC. Chứng minh \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \)
Giải:
* G là trọng tâm tam giác ABC \( \Rightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
* Ta có
\[\begin{array}{l}\overrightarrow {MA} = \overrightarrow {MG} + \overrightarrow {GA} \,\,\,\left( 1 \right)\\\overrightarrow {MB} = \overrightarrow {MG} + \overrightarrow {GB} \,\,\,\left( 2 \right)\\\overrightarrow {MC} = \overrightarrow {MG} + \overrightarrow {GC} \,\,\,\left( 3 \right)\\\left( 1 \right) + \left( 2 \right) + \left( 3 \right) \Rightarrow VT = 3\overrightarrow {MG} + \underbrace {\left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right)}_{\overrightarrow 0 } = VP\end{array}\]
Bài 4: Cho tam giác ABC và A’B’C’ có trọng tâm lần lượt là G và G’. Chứng minh \(\overrightarrow {AA'} + \overrightarrow {BB'} + \overrightarrow {CC'} = 3\overrightarrow {GG'} \)
Giải:
* Ta có:
\(\begin{array}{l}\overrightarrow {AA'} = \overrightarrow {AG} + \overrightarrow {GG'} + \overrightarrow {G'A'} \,\,\,\,\,\,\left( 1 \right)\\\overrightarrow {BB'} = \overrightarrow {BG} + \overrightarrow {GG'} + \overrightarrow {G'B'} \,\,\,\,\,\,\left( 2 \right)\\\overrightarrow {CC'} = \overrightarrow {CG} + \overrightarrow {GG'} + \overrightarrow {G'C'} \,\,\,\,\,\,\left( 3 \right)\\\left( 1 \right) + \left( 2 \right) + \left( 3 \right) \Rightarrow VT = 3\overrightarrow {GG'} + \left( {\overrightarrow {G'A'} + \overrightarrow {G'B'} + \overrightarrow {G'C'} } \right) - \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 3\overrightarrow {GG'} + \overrightarrow 0 - \overrightarrow 0 = 3\overrightarrow {GG'} \end{array}\)
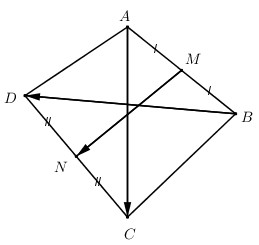
Bài 5: Tứ giác ABCD có M, N là trung điểm của AB, CD. O là trung điểm MN. Chứng minh :
a) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \)
b) I là điểm tùy ý. Chứng minh \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = 4\overrightarrow {IO} \)
Giải:
|
a) * Ta có: \(\begin{array}{l}\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OM} \,\,\,\,\left( 1 \right)\\\overrightarrow {OC} + \overrightarrow {OD} = 2\overrightarrow {ON} \,\,\,\,\left( 2 \right)\\\left( 1 \right) + \left( 2 \right) \Rightarrow VT = 2\left( {\overrightarrow {OM} + \overrightarrow {ON} } \right) = \overrightarrow 0 = VP.\end{array}\) b) * Ta có : \(\begin{array}{l}\overrightarrow {IA} = \overrightarrow {IO} + \overrightarrow {OA} \,\,\,\left( 1 \right)\\\overrightarrow {IB} = \overrightarrow {IO} + \overrightarrow {OB} \,\,\,\left( 2 \right)\\\overrightarrow {IC} = \overrightarrow {IO} + \overrightarrow {OC} \,\,\,\left( 3 \right)\\\overrightarrow {ID} = \overrightarrow {IO} + \overrightarrow {OD} \,\,\,\left( 4 \right)\\\left( 1 \right) + \left( 2 \right) + \left( 3 \right) + \left( 4 \right) \Rightarrow VT = 4\overrightarrow {IO} + \underbrace {\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right)}_{\overrightarrow 0 } = VP\end{array}\) |
|
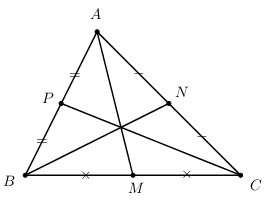
Bài 6 : Cho tam giác ABC, M, N, P là trung điểm của AB, BC, CA. Chứng minh \(\Delta MNP\) và \(\Delta ABC\) có cùng trọng tâm G.
Học sinh tự giải.
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
-
Lý thuyết cơ bản về vecto và bài tập áp dụng.(29/08)
Bài viết gồm những lý thuyết cơ bản nhất về vecto giúp các em nắm chắc kiến thức để có thể làm bài tập. Giúp các em không thấy bỡ ngỡ và không thấy sợ với những kiến thức mới khi bắt đầu bước vào lớp 10. Trong bài viết có những một số bài tập có lời giải chi tiết để các em học cách trình bày bài và những bài tập tự luyện để các em vận dụng.
-
Tọa độ Vectơ - Điểm(17/01)
Tổng hợp các kiến thức về vectơ, tọa độ điểm, có bài tập tự luận, trắc nghiệm vận dụng.