250 Bài tập trắc nghiệm đạo hàm tự luyện
Cập nhật lúc: 11:18 06-02-2017 Mục tin: LỚP 11
Xem thêm:
BÀI 1: ĐỊNH NGHĨA VÀ Ý NGHĨA CỦA ĐẠO HÀM
Câu 1: Cho hàm số f(x) liên tục tại \(x_{0}\). Đạo hàm của hàm f(x) tại \(x_{0}\) là:
A. \(f(x_{0})\)
B. \(\frac{f(x_{0}+h)-f(x_{0})}{h}\)
C. \(\lim_{h\rightarrow 0}\frac{f(x_{0}+h)-f(x_{0})}{h}\)( nếu tồn tại giới hạn)
D. \(\lim_{h\rightarrow 0}\frac{f(x_{0}+h)-f(x_{0}-h)}{h}\)( nếu tồn tại giới hạn)
Câu 2: Cho hàm số f(x) là hàm số trên R định bởi f(x)= \(x^{2}\) và \(x_{0}\in R\) . Chọn câu đúng:
A. \(f'(x_{0})=x_{0}\) B.\(f'(x_{0})=x_{0}^{2}\) C. \(f'(x_{0})=2x_{0}\) D. \(f'(x_{0})\) không tồn tại.
Câu 3: Hàm số f(x) xác định trên \(\left ( 0;+\infty \right )\) bởi \(f(x)=\frac{1}{x}\). Đạo hàm của f(x) tại \(x_{0}=\sqrt{2}\) là:
A \(\frac{1}{2}\) B. \(-\frac{1}{2}\) C. \(\frac{1}{\sqrt{2}}\) D.-\(\frac{1}{\sqrt{2}}\)
Câu 4: Phương trình tiếp tuyến của đồ thị hàm số y= \(\left ( x+1 \right )^{2}\left ( x-2 \right )\) tại điểm có hoành độ x=2 là :
A. y = -8x + 4 B. y = -9x + 18 C. y = -4x + 4 D. y = -8x + 18
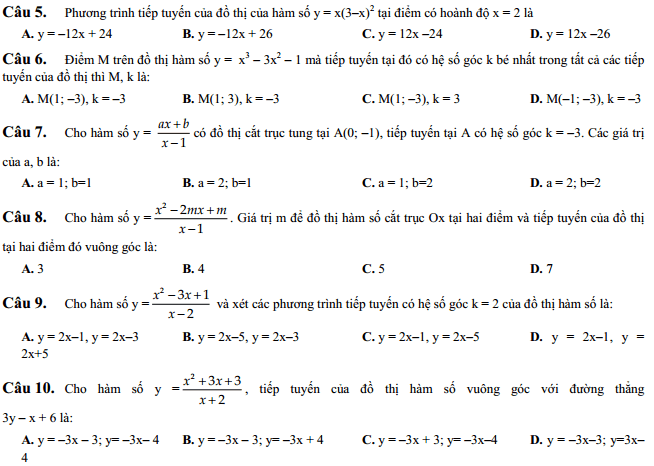








Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
-
Đạo hàm và các bài toán liên quan (đầy đủ; chi tiết)(10/03)
Tài liệu gồm 20 trang; trình bày về các dạng toán liên quan tới đạo hàm; gồm ba phần chính: Các công thức và bài tập về công thức tính đạo hàm; các bài tập về tiếp tuyến; các bài toán tính tổng. Tất cả các dạng toán đều nêu rõ phương pháp; các bài tập có lời giải chi tiết giúp các em học tập hiệu quả.

